Type 1 and Type 2 Errors in Statistics

Anytime we make a decision using statistics, there are four possible outcomes, with two representing correct decisions and two representing errors.

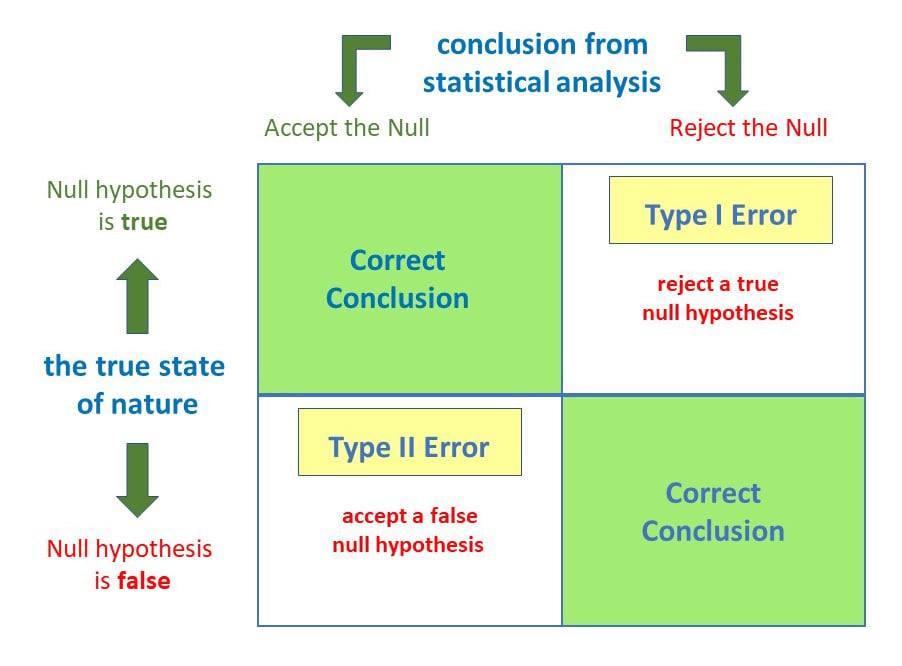
The chances of committing these two types of errors are inversely proportional: that is, decreasing type I error rate increases type II error rate and vice versa.

As the significance level (α) increases, it becomes easier to reject the null hypothesis, decreasing the chance of missing a real effect (Type II error, β). If the significance level (α) goes down, it becomes harder to reject the null hypothesis, increasing the chance of missing an effect while reducing the risk of falsely finding one (Type I error).

A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. Simply put, it’s a false alarm.

This means that you report that your findings are significant when they have occurred by chance.

The probability of making a type 1 error is represented by your alpha level (α), the p-value below which you reject the null hypothesis.

A p-value of 0.05 indicates that you are willing to accept a 5% chance of getting the observed data (or something more extreme) when the null hypothesis is true.

You can reduce your risk of committing a type 1 error by setting a lower alpha level (like α = 0.01). For example, a p-value of 0.01 would mean there is a 1% chance of committing a Type I error.

However, using a lower value for alpha means that you will be less likely to detect a true difference if one really exists (thus risking a type II error).

Example

Scenario: Drug Efficacy Study

Imagine a pharmaceutical company is testing a new drug, named “MediCure”, to determine if it’s more effective than a placebo at reducing fever. They experimented with two groups: one receives MediCure, and the other received a placebo.

• Null Hypothesis (H0): MediCure is no more effective at reducing fever than the placebo.
• Alternative Hypothesis (H1): MediCure is more effective at reducing fever than the placebo.

After conducting the study and analyzing the results, the researchers found a p-value of 0.04.

If they use an alpha (α) level of 0.05, this p-value is considered statistically significant, leading them to reject the null hypothesis and conclude that MediCure is more effective than the placebo.

However, MediCure has no actual effect, and the observed difference was due to random variation or some other confounding factor. In this case, the researchers have incorrectly rejected a true null hypothesis.

Error: The researchers have made a Type 1 error by concluding that MediCure is more effective when it isn’t.

Implications

1. Resource Allocation: Making a Type I error can lead to wastage of resources. If a business believes a new strategy is effective when it’s not (based on a Type I error), they might allocate significant financial and human resources toward that ineffective strategy.

2. Unnecessary Interventions: In medical trials, a Type I error might lead to the belief that a new treatment is effective when it isn’t. As a result, patients might undergo unnecessary treatments, risking potential side effects without any benefit.

3. Reputation and Credibility: For researchers, making repeated Type I errors can harm their professional reputation. If they frequently claim groundbreaking results that are later refuted, their credibility in the scientific community might diminish.

A type 2 error (or false negative) happens when you accept the null hypothesis when it should actually be rejected.

Here, a researcher concludes there is not a significant effect when actually there really is.

The probability of making a type II error is called Beta (β), which is related to the power of the statistical test (power = 1- β). You can decrease your risk of committing a type II error by ensuring your test has enough power.

You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.

Example

Scenario: Efficacy of a New Teaching Method

Educational psychologists are investigating the potential benefits of a new interactive teaching method, named “EduInteract”, which utilizes virtual reality (VR) technology to teach history to middle school students.

They hypothesize that this method will lead to better retention and understanding compared to the traditional textbook-based approach.

• Null Hypothesis (H0): The EduInteract VR teaching method does not result in significantly better retention and understanding of history content than the traditional textbook method.
• Alternative Hypothesis (H1): The EduInteract VR teaching method results in significantly better retention and understanding of history content than the traditional textbook method.

The researchers designed an experiment where one group of students learns a history module using the EduInteract VR method, while a control group learns the same module using a traditional textbook.

After a week, the student’s retention and understanding are tested using a standardized assessment.

Upon analyzing the results, the psychologists found a p-value of 0.06. Using an alpha (α) level of 0.05, this p-value isn’t statistically significant.

Therefore, they fail to reject the null hypothesis and conclude that the EduInteract VR method isn’t more effective than the traditional textbook approach.

However, let’s assume that in the real world, the EduInteract VR truly enhances retention and understanding, but the study failed to detect this benefit due to reasons like small sample size, variability in students’ prior knowledge, or perhaps the assessment wasn’t sensitive enough to detect the nuances of VR-based learning.

Error: By concluding that the EduInteract VR method isn’t more effective than the traditional method when it is, the researchers have made a Type 2 error.

This could prevent schools from adopting a potentially superior teaching method that might benefit students’ learning experiences.

Implications

1. Missed Opportunities: A Type II error can lead to missed opportunities for improvement or innovation. For example, in education, if a more effective teaching method is overlooked because of a Type II error, students might miss out on a better learning experience.

2. Potential Risks: In healthcare, a Type II error might mean overlooking a harmful side effect of a medication because the research didn’t detect its harmful impacts. As a result, patients might continue using a harmful treatment.

3. Stagnation: In the business world, making a Type II error can result in continued investment in outdated or less efficient methods. This can lead to stagnation and the inability to compete effectively in the marketplace.