In statistics, a sampling distribution is the probability distribution of a statistic (such as the mean) derived from all possible samples of a given size from a population.
The sampling distribution of a given population is the distribution of frequencies of a range of different outcomes that could possibly occur for a statistic of a population.
In statistics, a sampling distribution shows how a sample statistic, like the mean, varies across many random samples from a population. It helps make predictions about the whole population. For large samples, the central limit theorem ensures it often looks like a normal distribution.
Purpose of Sampling Distributions
Sample statistics only estimate population parameters, such as the mean or standard deviation. This is because, in real-world research, only a sample of cases is selected from the population.
Due to time restraints and practical issues, a researcher cannot test the total population. Therefore, it is likely that the sample mean will be different from the (unknown) population mean.
However, a researcher will never know the exact amount of sampling error, but by using a sampling distribution, they can estimate the sampling error.
Three different distributions are involved in building the sampling distribution.
- Population Distribution: The distribution of all individual values or items in the entire population (N).
- Sample Distributions: Distributions of various random samples taken from the population (n). while the concept of “all possible samples” underlies the idea of a sampling distribution, we don’t actually select an infinite number in practice.
- Sampling Distribution: The distribution of a particular statistic (like the mean) calculated from each of the possible samples.
How to Find Sampling Distribution
It is important to note that sampling distributions are theoretical, and the researcher does not select an infinite number of samples.
- Start with the Population: Ideally, know the entire population and its parameters (N). However, in many cases, this is impractical or impossible.
- Choose a Sample Size: Determine the size of your sample, denoted as .
To create a sampling distribution, research must:
- Draw Random Samples: Randomly select numerous samples of size from the population. This process is repeated many times, each time selecting a new sample and calculating its mean. The distribution of these sample means constitutes the sampling distribution of the sample mean.
- Calculate Sample Statistic: For each sample, calculate the desired statistic (e.g., mean).
- Determine the Difference: Calculate the difference between the sample means for each sample drawn. The magnitude of the difference can be influenced by the sample size. Larger samples often provide more reliable and stable estimates of the population mean, leading to a narrower distribution of differences.
- Construct the Distribution: Plot the differences in sample means to visualize their distribution, and compute related statistics (e.g., mean of the differences, standard error of the difference) to characterize this distribution.
The Central Limit Theorem
In practical applications, it’s not feasible to draw infinite samples to create a sampling distribution. However, the concept of drawing “all possible samples” is a theoretical foundation underlying the idea of a sampling distribution.
In practice, the properties of the sampling distribution (like its mean and standard error) are often inferred using statistical theory and data from a single sample, aided by principles such as the central limit theorem.
The central limit theorem tells us that no matter the population distribution, the sampling distribution’s shape will approach normality as the sample size (N) increases.
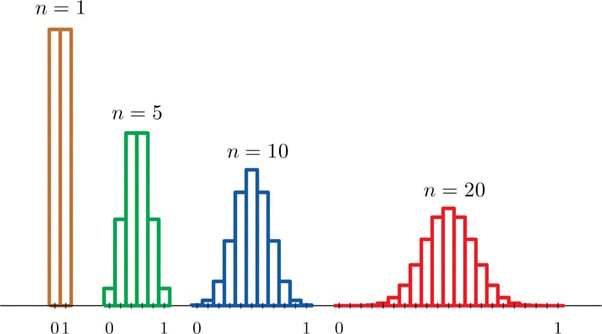
Figure 1. Distributions of the sampling mean (Publisher: Saylor Academy).
This is useful, as the research never knows which mean in the sampling distribution is the same as the population mean, but by selecting many random samples from a population, the sample means will cluster together, allowing the research to make a very good estimate of the population mean.
Thus, the sampling error will decrease as the sample size (n) increases.
The Central Limit Theorem provides a foundation for many statistical procedures and inferences by ensuring that the sampling distribution of the sample mean becomes predictable (normally distributed) when the sample size is large.

